Time Complexity Analysis
In this post, we will do some excise to understand the actual significance of asymptotic notation. How, we will calculate the complexity and what will be the notations. The following series are important before we can begin to calculate the complexity.
Linear series (arithmetic series) for n>=0
Quadratic series for n>=0
Cubic series for n>=0
Geometric series for x!=1,
For |x|<1 nbsp="" span="">
Linear Geometric series for n>=0, real c!=1
Harmonic series nth harmonic number
The unrolling of the looping statement within the computer programs may resemble with the following series, and we can directly use it to compute the complexity of the scheme.
How to define notations
Linear series (arithmetic series) for n>=0
Quadratic series for n>=0
Cubic series for n>=0
Geometric series for x!=1,
For |x|<1 nbsp="" span="">
Linear Geometric series for n>=0, real c!=1
Harmonic series nth harmonic number
The unrolling of the looping statement within the computer programs may resemble with the following series, and we can directly use it to compute the complexity of the scheme.
How to define notations
- Normally, the time complexity with worst case analysis is important
- If the complexity of Worst case (Big-O) == Best cast (Big-Omega), than we can go with Average case complexity i.e (Big-theta)
- If the loops in the problems are independent, then multiplication of their final run will give the complexity.
- if loops in a given problem are dependent, then unrolling is important and the last loop unrolling is consider to calculate the complexity Independent loops based problem:A(){int i;for(i=1 to n) % last run n timesfor(j=1 to n) % last run n timespf("munna");}In the above problem loops are independent, hence its complexity will be the multiplication of the loopsTime Complexity= n x n , then O(n^2)Dependent loops based problem:Few points remember when solving the problem
- If loop iteration is not sequential, than assume k times loop will take to get executed
- See the increment pattern, and map with the above series
A(){int i=1, s=1; Increment in serieswhile(s<=n) s:=1 3 6 10 15 21{ i:= 1 2 3 4 5 6i++s=s+i;pf("deepa")}}In the above problem, the s incremental is in the form of sum of first two natural number. Hence, the linear series is the most appropriate resemblance with the above problem.However, the running of the loop is not sequential and dependent on the value of the s. In the program while loop hold some condition, where the loop will be stop when the s value will greater than or equal to the value of n.Therefore, we assume after the k iteration the loop will stop and program will end. To represent the s series in the form of k, we assume the k in place of s in the while loop and say after k iteration looping get to end:So time complexity in terms of k = k(k+1)/2 ) (sum of first two natural number)However, we need time complexity in terms of n. Therefore, see the condition given in the while loop and say when the k will be greater than or equal to the n then the loops gets complete execution.Sok(k+1)/2>=nsimplify the above relationk^2+k>=2nhence,k=⎷nThe time complexity in terms of n will be = ⎷n





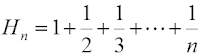




Comments
Post a Comment